Venice Math Circle

We have many, many of these dinosaurs which come in six species and six colors (so how many possible dinosaurs are there?).

For this lesson, Sami selected a handful of dinosaurs and laid out two ropes formed into circles on the floor. First up, put all red dinosaurs in the red circle and all blue dinosaurs in the black circle. No problem! Second up, all triceratops in the red circle and all brontosauruses in the black circle. Easy peasy!

Then Sami asked the children to sort all of the red dinosaurs into one circle and all of the T-rex dinosaurs into the other. After a flurry of flying dinos, the children started to see the problem… where, oh where, should the red T-rex go? In the red circle since it’s red? In the T-rex circle since it’s a T-rex?

After much deliberation as to whether putting the red T-rex into either circle truly satisfied the objective, one child suggested the red T-rex had to go in the middle, between the two circles. The group was unsatisfied with this solution. Then another child suggested they move both circles until that red T-rex was inside of both, thus creating a Venn Diagram of dinosaurs. Everyone agreed this was the best solution.

Of course, we didn’t stop there. Sami next asked the children to count the number of red dinosaurs (4) and the number of T-rexes (4) and then asked, how many dinosaurs total? The children all agreed that there must be 4+4=8. So we counted. And got 7… interesting!

Boon makes wonderful bath toys, including a fleet of stackable boats
that come in handy for transporting dinosaurs across a scarf river, which was the main focus of the following activity.

To begin, each child selected a boat and Sami asked them to assemble a “set” of three dinosaurs, in which two are the same color and two are the same species. Once each set was selected, we used two circles to test the solution, where one circle had both of the same color, the other both of the same species, and one dinosaur in the overlapping intersection. With passengers assembled, the boats lined up on one side of a flowing scarf and prepared to cross the river.

Round 1: At least one and at most two dinosaurs must be in the boat for every crossing. The children had no trouble puzzling this one out, and all dinosaurs made it to the shore with three crossings (two forward, one back).

Round 2: No two dinosaurs of the same color may ride in the boat together. After a couple turn-around trips across the sea, the captains sailed their dinosaurs safely across.

Round 3: No two dinosaurs of the same color or of the same species may ride in the boat together. This one took a fair amount of puzzling and some dinosaurs took an inevitable swim in the river, but in the end, the children mastered this colorful twist on the classic river crossing puzzle.

On this day we began with a story about a house with many stories (because no one is too young to appreciate puns).

Hermie is a precocious little girl who lives on the top floor of a nine story building. Each morning she rides the elevator all the way down to the first floor. Each evening she rides the elevator up to the fourth floor, then takes the stairs the rest of the way. How strange! Why does she do that?

Conjectures included a play date with a friend, a desire to run super fast up the stairs, and that she didn’t like the dog in the elevator. The story continued…

Several months later, Hermie rides down to the first floor in the morning, and rides up to the fifth floor before taking the stairs to the ninth in the evenings. What, oh what, is going on?

Conjectures again included the barking elevator dog, but now also that she was more tired than usual. So Sami had the kids come to the white board one at a time to try to push the red elevator buttons. They managed to push 5 just fine, but none could reach up to 9. The story ended with the riddle solved, but class was far from over.

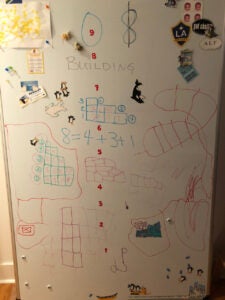
Sami gave each child two dozen wooden cubes, which we called “rooms”, and asked them to build houses with 4 rooms and 2 stories. We discovered that there were only 2 ways to do it. We counted the rooms by floor, 2+2 and 3+1, so we found two ways to add up two numbers to get 4. Then we moved on to how many different buildings we could make from 5 rooms with any number of floors, and we discovered there are exactly 7 integer partitions of 5 (once we left justified our rooms, of course).

Next up, how many buildings can we make from 8 rooms with exactly three stories? Some kids stuck with blocks on the floor with Sami, others took over the white board to draw buildings as Young diagrams with Sabrina, but everyone built masterpieces with exciting stories about who lives there and when they can have a play date with Hermie!