Unlocking the Secrets of a 4D Cosmos
Key points
Pushing the boundaries of knowledge to better understand how our universe works, a USC Dornsife-led project may create advances now considered science fiction.
The four-year project, funded by an $8 million Simons Foundation grant, brings together researchers from 11 prestigious institutions to tackle some of the most pressing questions in mathematics and theoretical physics.
A key distinction of this type of funding: It aims to extend the boundaries of knowledge by assembling scientists, researchers and scholars who don’t typically interact.
This story involves two kinds of math: simple and very complex.
The simple math adds up to an exceptional amount of money — $8 million, in fact — to study the other, more complex math over the next four years. That’s $2 million per year, and a few more digits than are typically found on grants awarded for math research.
Most grants funding science go to experimental equipment, postdoctoral scholars, graduate students and other expensive resources.
“In math, all we typically need is a paper and pencil, so grants tend to be much less,” says Aaron Lauda, professor of mathematics and physics and astronomy at the USC Dornsife College of Letters, Arts and Sciences. Lauda led the charge to obtain the prestigious grant, which establishes the Simons Collaboration on New Structures in Low-Dimensional Topology.
The grant is unique in that it is sufficiently large to fund a sizable team working in a similar direction and will support extended visits by team members and other experts that will enhance the research activities and community at USC, says Lauda, who directs the collaboration.
The funding comes from the Simons Foundation. Lauda as director, along with grant co-principal investigator Cris Negron, assistant professor of mathematics, brings nearly 14% of the total — about $1.1 million — to USC. It’s one of the largest awards ever obtained for USC Dornsife’s math department.
The remaining $6.9 million is divided among 10 other institutions: Caltech, the Massachusetts Institute of Technology, UCLA, the University of North Carolina at Chapel Hill, and Columbia, Stanford, Princeton and Harvard universities, as well as the Centre for Quantum Mathematics at Southern Denmark University and the University of Zurich.
Simons collaboration aims to solve knotty math problems
The complex math that Lauda and the other researchers are exploring centers on topology. In vastly oversimplified language, topology refers to the properties of a geometric shape that don’t change no matter how much you futz with it.
Lauda points to knots as an example.
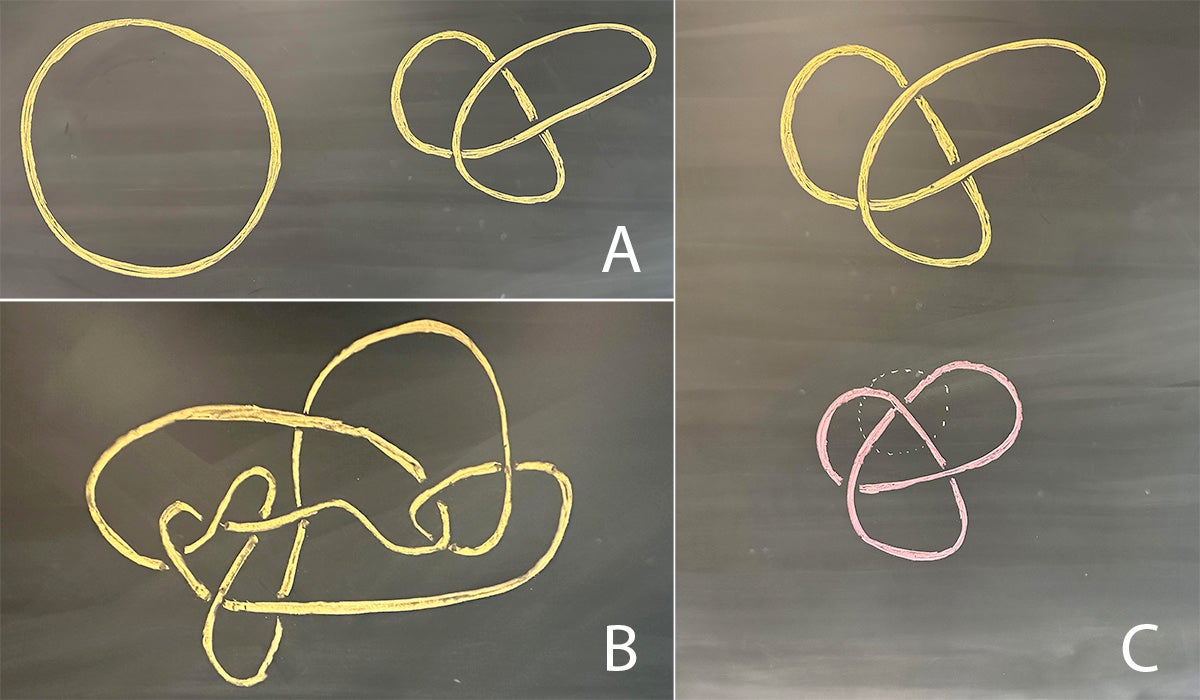
A length of rope twisted and tangled, and then joined at the ends to make a single, contiguous knot, has its own topology. No matter how the knot is positioned, it’s still the same knot.
“If I wiggle it around, as long as I don’t cut it or break it, it’s fundamentally the same,” Lauda says.
And if two people arbitrarily twist and tangle separate but identical ropes of the same size and seal the ends together, even the most discerning eye might have difficulty determining if the two knots are the same or different.
As Lauda explains it, we can try to wiggle one knot to look the same as the other, but if we don’t succeed, we can’t necessarily conclude that the two knots are different. Perhaps we didn’t try hard enough. This is where the mathematics of knot invariants can help.
A knot invariant is a way of assigning a number or polynomial to a knot that stays the same no matter how the knot is wiggled or deformed. If our invariant assigns different numbers, or polynomials, to two different knots, then we can be certain that the two knots are different.
Mathematicians push for advances on par with Einstein’s
As fun as knots can be, Lauda and his project collaborators have set their sights on more grandiose issues of topology, aiming to build on existing theory and tools to answer fundamental questions about the universe.
“Knot theory is interesting because it’s an intersection point where ideas from theoretical physics, like string theory, intersect with some of our more sophisticated mathematical tools,” Lauda says. “But what the collaboration is really trying to do goes way beyond knots, to understand the ways in which even our reality can have these types of topological properties.”
Lauda refers to knowledge on par with that revealed by Einstein and his General Theory of Relativity, which shows that the three dimensions of space are intimately linked with a fourth dimension, that of time. And mass — planets, stars and even knots — warp space-time, something we experience as gravity.
In revealing the gravitational curvature of space-time, Einstein revolutionized perceptions of the universe, and this in turn made technologies such as GPS navigation possible.
Lauda says that, when it comes to topology, accounting for that fourth dimension has led to important advances in math and physics, and he and his collaborators aim to push the boundaries of knowledge.
“Mathematically, it’s important to understand and classify four-dimensional topological objects in the same way we do knots,” he says. “That’s the sort of big frontier we’re trying to accomplish with this collaboration.”
Math collaborators work toward advances in four dimensions
Mathematicians trying to describe spacetime do so by specifying four dimensions: three spatial dimensions (up and down, back and forth, right and left) and one time dimension.
For mathematicians and physicists, working on that fourth dimension proves most challenging, a fact Lauda finds intriguing. “It is a curious fact of nature that dimension four is unique in that our understanding is vastly limited in precisely this dimension that just so happens to coincide with the four dimensions that compose our universe.”
In other words, time is really weird. So weird that even the brightest minds struggle to get a handle on it.
The Simons Collaboration aims to tackle this confounding dimension head on, developing the next generation of tools for studying four-dimensional topology, unlocking new techniques arising from theoretical physics and resolving long-standing questions that have plagued mathematicians for decades, Lauda says.
For example, the project could shed important new light on the theories for quantum gravity, or a theory that combines general relativity and quantum physics.
“General relativity works fantastically when you’re talking about planets, stars and the like,” Lauda explains. “Quantum mechanics works when you’re talking about very small things like subatomic particles. But once you start combining those small things with the big things, like one might encounter near a black hole, or near the big bang, the theories start breaking down.”
He says the project’s efforts could set the stage for finally closing the divide, giving deeper insight into how the universe works at all levels.
What’s more, any breakthroughs in understanding could lead to scientific and technological advances in the same way Einstein’s discoveries led to GPS, he says.
“What we expect to learn from this project could be the foundation for future technologies and advances that seem like pure science fiction now.”